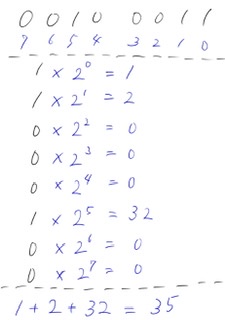2進数
コンピュータは全ての数を0と1のみで表現する。対して人間は0〜9までの数字を使って数を表現する。0〜9をで表現する数を10進数、それに対し0、1のみで表現する数を2進数という。
10進数と2進数の対比を以下に示す。
| 10進数 | 2進数 |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
10進数は、0,1,2…と進んで行き9まで来ると桁上がりして10となる。10進数の10から1を引いた数”9”まで来ると桁上がりする。
2進数は、2から1を引いた数”1”まで来ると桁上がりする。つまり全ての桁が1になると桁上がりをする。例えば1の次は桁上がりして10となる。ちなみに2進数の10は”ジュウ”ではない。10と書いて”イチゼロ”とか”イチマル”と言う。
ここで、10と書いても10進数のジュウなのか、2進数のイチゼロなのか区別がつかないため、普通は10進数の場合は頭に”d”をつけてd10のように書き、2進数の場合は頭に”0b”をつけて0b10と書く。dはデシマルの略、bはバイナリの略である。10進数のdは省略する場合が多い(と思う)。
2進数の場合、1桁を”bit(ビット)”という。bitというのがコンピュータで数を表す最小単位となる。0b10は2bitだし、0b1111は4bitである。
bitが8つ集まった8bitの事を”Byte(バイト)”という。0b11111111は1Byteである。
コンピュータで2進数を扱う場合、表記を1Byte単位に合わせて書く場合がある。0b1なら0b0000 0001、0b11110なら0b0001 1110と書く。この際4bit毎にスペースを入れて書くと読みやすくなる。(理由は後の16進数の項目で説明する)
10進数と2進数の変換
・10進数から2進数へ
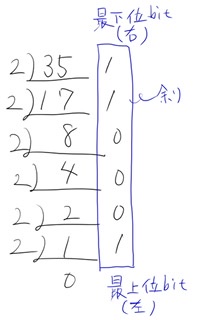
10進数を2進数に変換するには、変換したい10進数の数字を商が0になるまで2で割り続け、余りを求めていく。求められた余りが変換後の2進数となる。
例えば35を2進数に変換すると、0b0010 0011となる。
・2進数から10進数へ
2進数から10進数に変換するには、各bitの値にその桁の「重み」を掛ける。重みという言葉が出てきたが、n桁目の重みは2のn-1乗となる。例えば、3桁目の重みは2の2乗となって4である。そして最後に各桁で算出した値を足し合わせる。
先ほどの0b0010 0011を10進数に変換すると、下記の通り35となる。